极简机器学习入门指南

原文作者：Dan Harris

翻译：Jesse

整理：阳哥

译文出品：Python数据之道（PyDataLab）

机器学习背后的术语可能听起来很复杂，但概念非常直观

近几年，像“机器学习( Machine Learning )”，“深度学习( Deep Learning )”，“神经网络( Neural Network )”，“人工智能( Artificial Intelligence )”或“人工智能( A.I )”，“数据科学( Data Science )”等词语在科技界已成为流行术语。 由于计算能力提高和可用数据量增加，现在可以将已知数十年的科学技术应用到实践中来。

但是这些术语究竟是什么意思？

数学公式让机器拥有像人类一样基本的理解能力

我们大多数人都可以意识到 1 万多行的解释说明“全部是为了教电脑去帮助我们解决问题” ，但许多人可能不知道实际发生了什么。 机器学习的基础知识非常简单，足够直观，而且更重要的是，足够有趣，让每个人在相对较短的时间内理解它。

下面我们将简单介绍如何使用机器学习来教电脑解决问题，是为了针对那些不了解机器学习的人或那些想要从头开始的人。

最佳拟合线 (The Line of Best Fit)

我们中的许多人可能会记得来自学校的一些东西，称为“最佳拟合线”，参考绘制在图表上的数据点。 最佳拟合线是一条通过这些点的线，它用来表示数据表达的内容。 它可能看起来像这样：

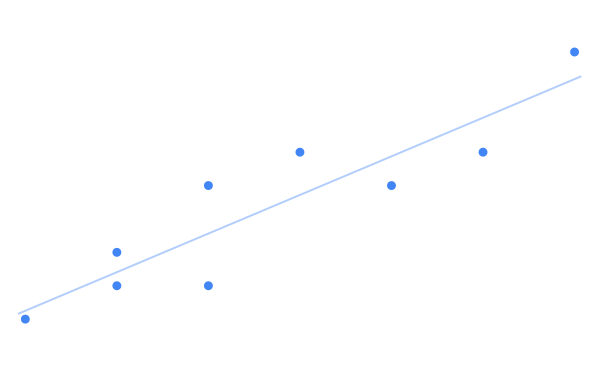
这个概念实际上是最基本的机器学习。 我们可以将数据提供给计算机，而不是自己绘制这些点并尝试绘制出最佳拟合线。

例如，可以想象上图中显示的数据是一些人的鞋子尺寸和身高。 左下角的点表示这个人的身高比其他人矮并且鞋子尺寸比其他人小，右上角的点表示这个人较高且脚较大。 因为鞋子的尺寸和高度并不是完全相关，所以不是所有的点都符合“较高的人有较大的脚”的说法，但最适合的线条表明它在一般情况下是正确的。

通过最佳拟合线，我们可以对新数据做出有根据的猜测。 假设你找到了一双鞋子。 您可以确定它的大小，然后参考相关图表，对鞋子主人的身高做出有相关的猜测：

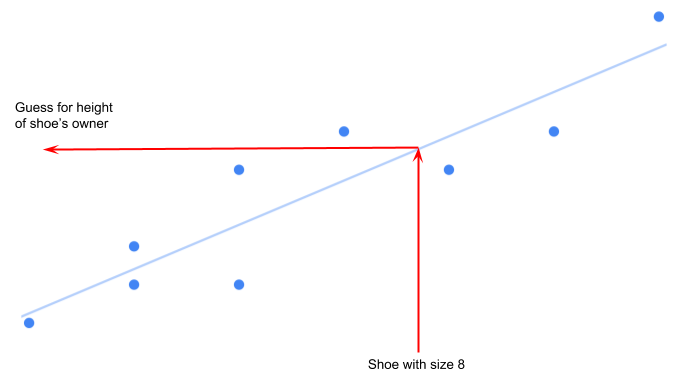
简单吧？ 在机器学习中，这被称为“线性回归”，不要让名字吓到你。 如果你了解上述所有内容，那么就会理解线性回归。 这是一种简单的机器学习技术，用于帮助对具有线性关系的数据进行预测。

机器学习的线性回归过程如下：

1. 收集数据；
2. 将数据导入进程序，用线性回归分析这些数据并画出最佳拟合线；
3. 使用最佳拟合线来预测新数据。

这些被称为“机器学习”，因为计算机（或机器）已经学习了（或创建了一个数学公式，在这种情况下，是一条线）怎样联系鞋子的尺寸和身高的关系。 数学方程使机器基本理解了我们作为人类学到的东西：一般来说，较高的人有较大的脚。

在其他情况下，你可以根据房子的房间数并用线性回归来猜测房屋的成本，或根据他们在圣诞树下有多少礼物来猜测孩子有多少阿姨和叔叔。

线性回归问题

当数据成线性关系时，线性回归效果显著，如以上例子。但它处理看起来不成线性关系的数据效果会怎么样？也许数据看起来像这样：

添加最佳拟合线，效果图如下：

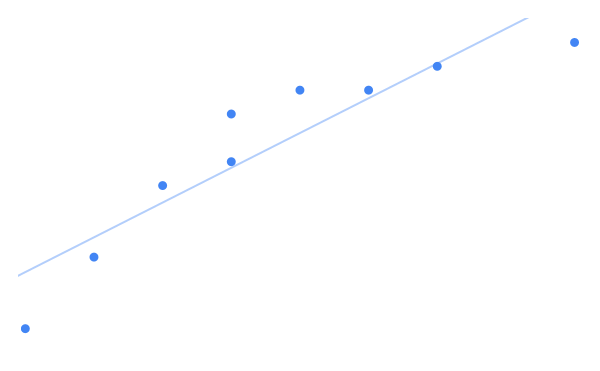
最佳拟合线匹配数据效果还可以接受，但似乎它可以做得更好。因为数据的形状不是一条直线，因此绘制的最佳拟合线不适合数据。这是机器学习中的一个问题，称为“欠拟合”：最佳拟合线并不能很好地拟合数据。但是如果我们弯曲最佳拟合线，它可能会做得更好。

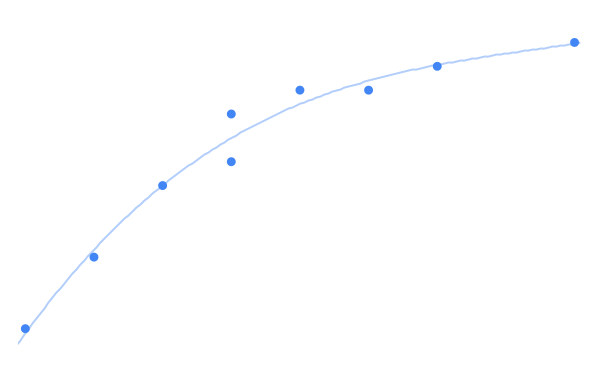
我们可以轻松利用曲线使数据拟合更准确，上图方法就像我们用直线的最佳拟合一样。这是一个简单的线性回归扩展，称为“多项式回归”。再次，不要让名字吓到你。如果你理解为什么曲线拟图时比直线更有准确，那么你就能理解多项式回归是如何有用。

现在我们可以创建一个模型，即：对于具有直线或曲线形状的数据，找到一组数据的最佳拟合线或曲线。这些内容上面已经介绍了，对吧？ 但并未结束，我们可以在这些概念之上进行拓展。

选择模型的准确度

多项式回归的问题是我们必须在使用它之前决定给它的次数（幂的次数），这可能很棘手。让我们回到我们的第一组数据：

我们以前使用线性回归在这些数据点之间画一条直线。但相反，我们可以使用多项式回归将最佳拟合曲线放在数据点之间，效果有可能比线性回归显著。它可能看起来像这样：

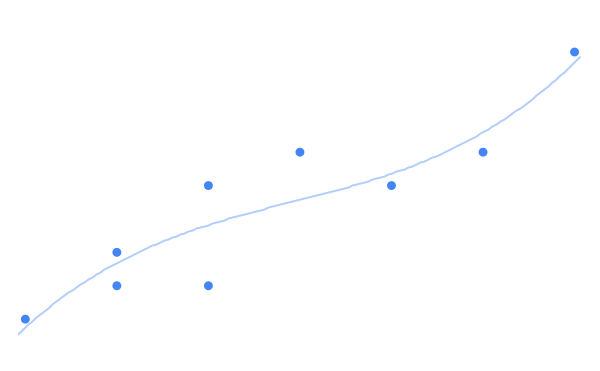
关于多项式回归，我们可以设定最佳拟合曲线的准确度。次数越高，它在描述数据集时就越灵活。上面最合适的曲线非常简单，但可以进一步拟合数据，如下所示：

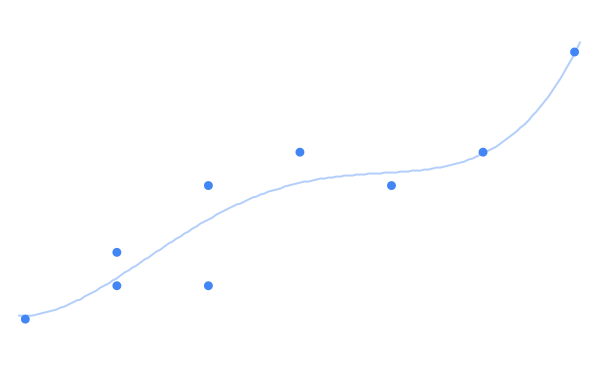
或者如下图拟合数据：

上面的最合适曲线似乎越来越准确地描述数据，但有些东西有点感觉不对，特别是在最后一个例子中。最佳拟合曲线的灵活度越高，它就很难把一些数据点连接起来。结果是一条曲线对于预测而言似乎不如最佳拟合直线。

我们再次回到鞋子尺寸和高度例子中，我们可以看到两个不同鞋尺寸的人在最佳拟合曲线中有着相同的身高：

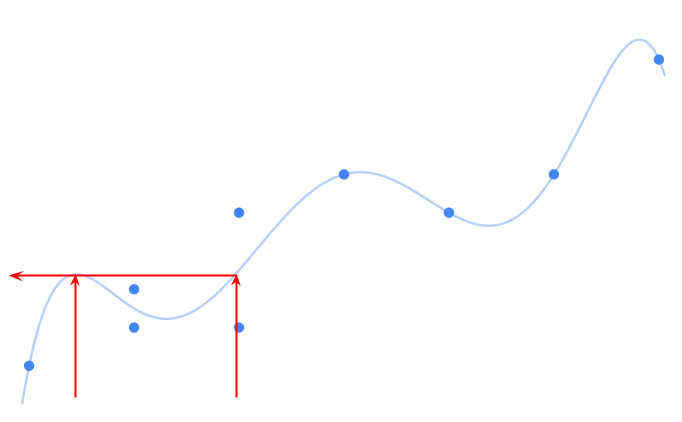
机器学习中的这个问题被称为“过度拟合”，与欠拟合相反。这意味着我们创建的最合适的曲线并不能很好的代表整个数据概况。它在连接数据点上面做的不错，但它无法于对任何新数据做出准确的预测。机器学习的主要问题之一是找到最合适的线条或曲线，其曲率足以模仿数据的一般规律形状，但不是那么弯曲，以至于无法对新数据进行良好预测。

这是多项式回归容易出现的问题。在拟合数据之前我们必须明确多项式回归使拟合曲线的弯曲程度，这不是一件容易的事情，尤其是当数据更复杂时。

在到目前为止的示例中，我们的数据只有两个维度 - 例如鞋子尺寸和身高 - 这意味着我们已经能够在二维图上表达我们的数据。二维图很容易看到数据的一般形状。但是，在具有两个以上维度的机器学习问题中通常不会出现这种情况。如果我们不知道数据的形状是什么，我们就不能准确的确认多项式回归曲线的次数去制作最合适的线条。

进一步挖掘，神经网络也可用于回答关于数据的是与否问题而不是返回数字。

一种选择是多次尝试多项式回归不同的幂次数据，并观察哪个次数效果最好。但我们真正需要的是机器学习既可以满足线性拟合的灵活性，同时也限制它的曲率，以便能够更好地应用于新数据。

研究人员通常通过从线性和多项式回归转向使用神经网络来解决曲线灵活性问题 。就其本身而言，神经网络非常类似于多项式回归，因为它能够学习具有非常弯曲形状的数据。它们并没有解决自身产生的过度拟合的问题，但当与一种称为正则化的技术相结合时，一切都趋于成功。

神经网络和正则化使用细节对于理解机器学习的基础知识并不是非常重要。需要记住的关键事项是，神经网络非常擅长学习复杂数据集的形状 - 比线性或多项式回归更有效 - 和正则化有助于防止神经网络过度拟合数据。

让电脑回答问题

对于迄今为止所涉及的技术 - 线性回归，多项式回归和神经网络 - 我们只研究了如何根据我们提供的数据训练计算机给我们一个数字。鞋子尺寸和身高模型可以告诉我们相应的身高数据根据我们输入的鞋子尺寸。类似地，根据房间数量的房价模型，我们可以知道房子价格当我们给出了房间数。

但是数字输出并不总是我们想要的。有时我们想要机器学习模型来回答问题。例如，如果你想卖房子，你可能不会只关心机器学习计算出你房子的价值，但你可能还想知道房子是否会在六周内售出。

好消息是许多机器学习技术可以解决回答特定问题而不是给出数字的问题 ，类似于我们已经介绍的技术 。当我们提供一些基本输入数据（如房间数量，成本和平方英尺）时，可以设置机器学习模型以给出六周内销售问题的是/否答案。显然，它永远不会是一个完美的模型，因为住房市场不遵循确切的规则，但机器学习模型可以给出这些类型问题很精确的答案（取决于数据的质量）。

对于线性回归，所涉及的是线性形式的逻辑回归。（同样，不要让术语使你害怕。基本方法实际上非常直观。）它可以回答诸如“这封垃圾邮件是垃圾吗？”或“明天会下雨吗？”。两种方法 - 线性和逻辑回归 - 会计算一条最佳拟合线，但它们在使用该线时的方式不同。提醒一下，这里我们使用线性回归模型是为了预测其它的数据：

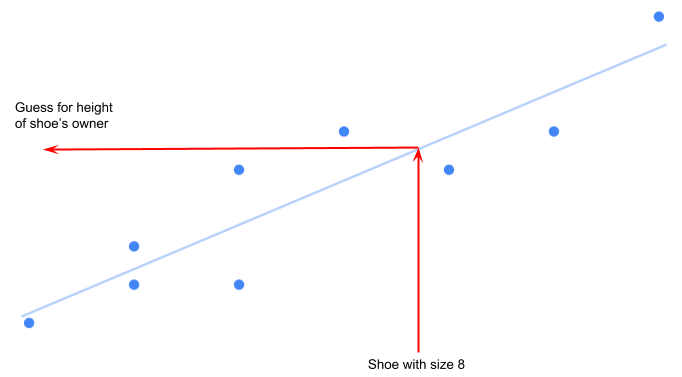
逻辑回归与之前的方法有些类似，不同的是找到了一条最佳拟合线的同时也将数据分成两组。然后，该线可用于预测新数据点是位于这个组还是另一个组中，具体取决于它所在线的哪一侧。

像线性回归一样，逻辑回归可以扩展为使用弯曲的多项式模型，该模型在拟合数据形状方面具有更大的灵活性。通过一点额外的扩展，神经网络也可用于回答关于数据的是/否问题而不是返回数字。

如果我们想要回答比寻找是/否更复杂的问题，我们可以使用多项逻辑回归，或者我们也可以调整神经网络以便能够处理这些情况。以这种方式创建的模型将能够回答诸如“明天会下雨，晴天还是下雪？”这样的问题。“多项”部分只是意味着答案可以是众多选项之一。在该示例中，三个可能的答案将是下雨，晴天或下雪。

原文： https://medium.com/s/story/machine-learning-for-people-who-know-nothing-about-machine-learning-fcc312a53f12

对我的文章感兴趣的朋友，可以关注我的微信公众号「Python数据之道」（ID：PyDataLab），接收我的更新通知。